Mandlebrot Set Generator

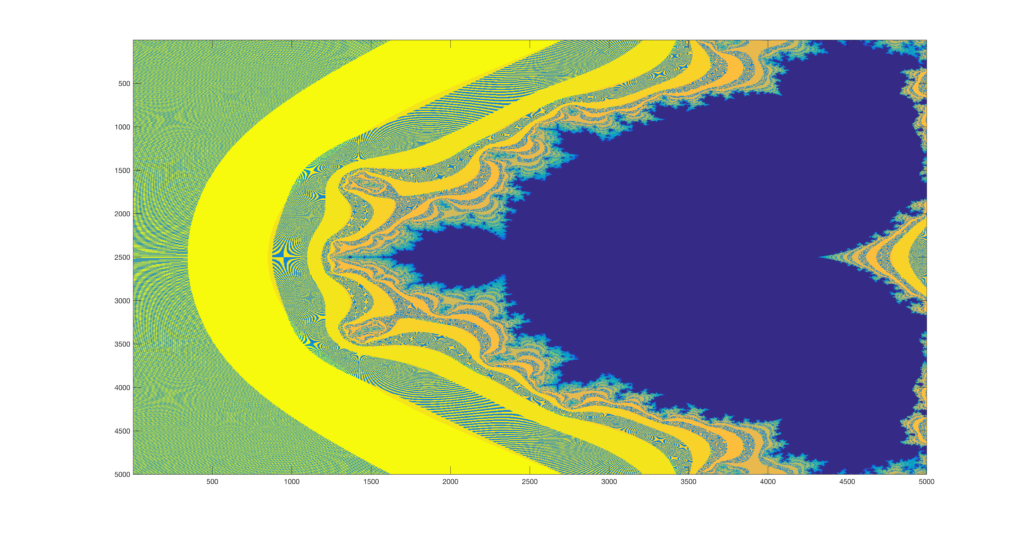
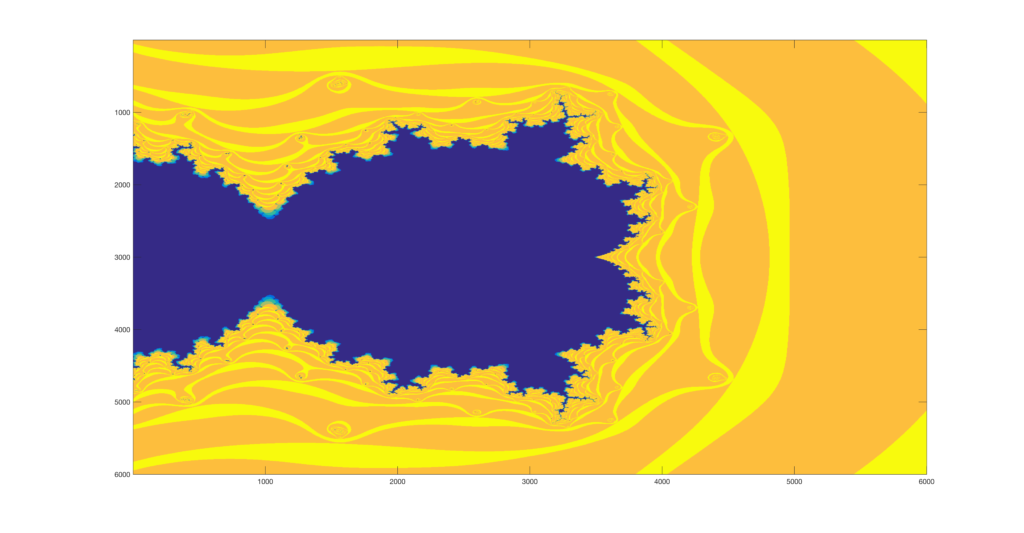
I was playing around with the Mandlebrot set yesterday in Matlab, and eventually after iterating on my implementation of it, decided to take a few photos and screencaps of deep zooms on particular points. I have been having a bit of a hard time identifying the right points to zoom in on but was still able to arrive at a few pretty nice ones. At the end of this gallery I will also provide my very short code that can generate these.

3
First, the famous Mandlebrot set in all it’s glory!
23
I began playing around with the recursive function that generates the set by adding polynomial terms of higher order.
25
I also played around with the various thresholds I could use to assess convergence of the set at all the points in the image.
22
This one is particularly surprising in the minimal amount of chaotic behavior and the elegant structuring of the self-similar pattern.
5
I find this one to be very lovely with its soothing colors and faded aesthetic.
20
A highly structured higher-order polynomial cousin of the Mandlebrot family
7
A low-res version with many different thresholding layers to achieve the coloring pattern you see there.
21
More varieties, this is getting really fun!

15 14

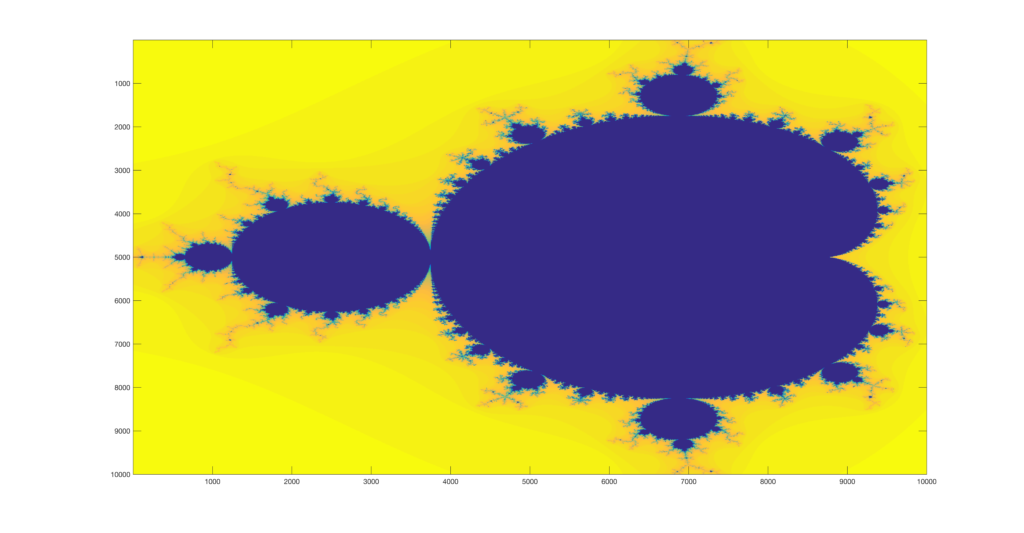
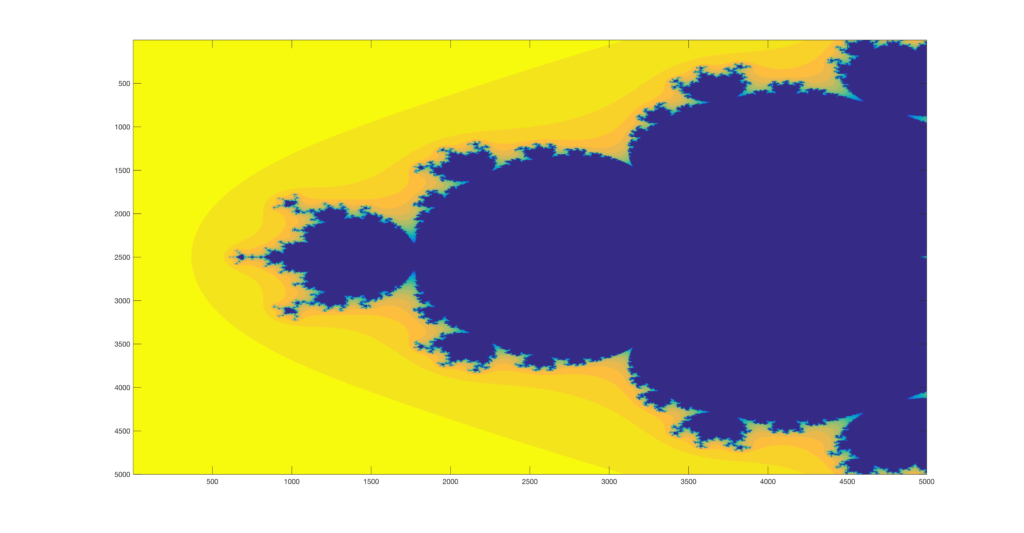
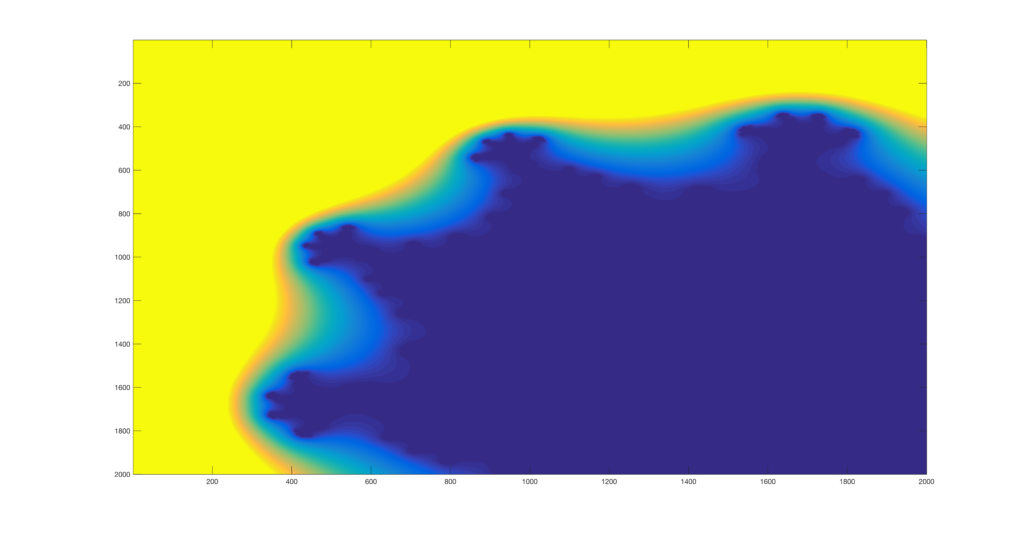
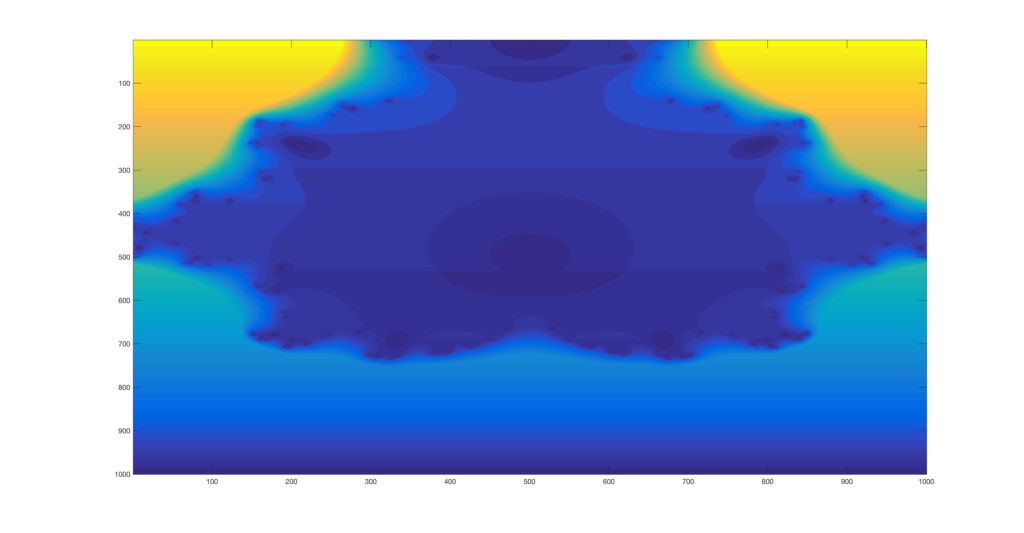
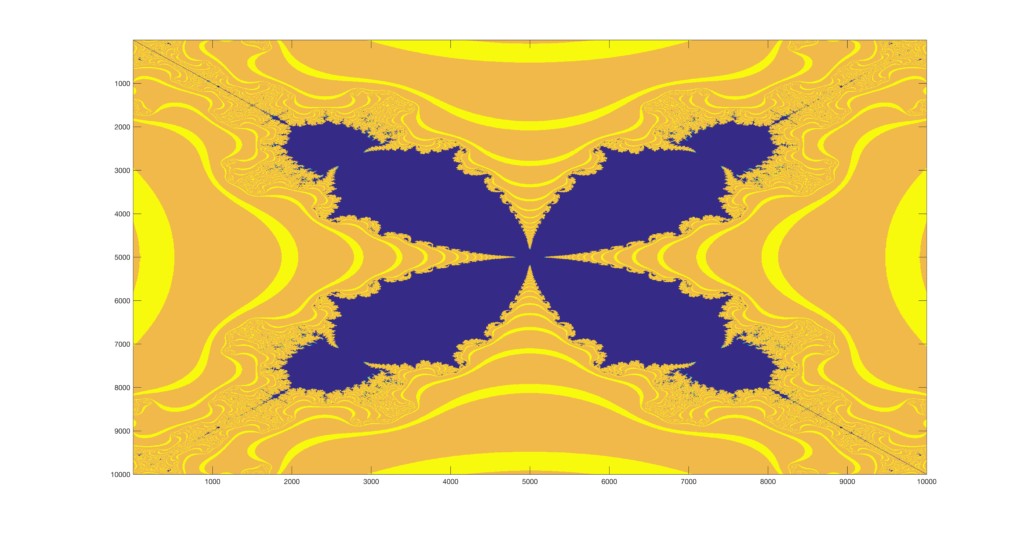
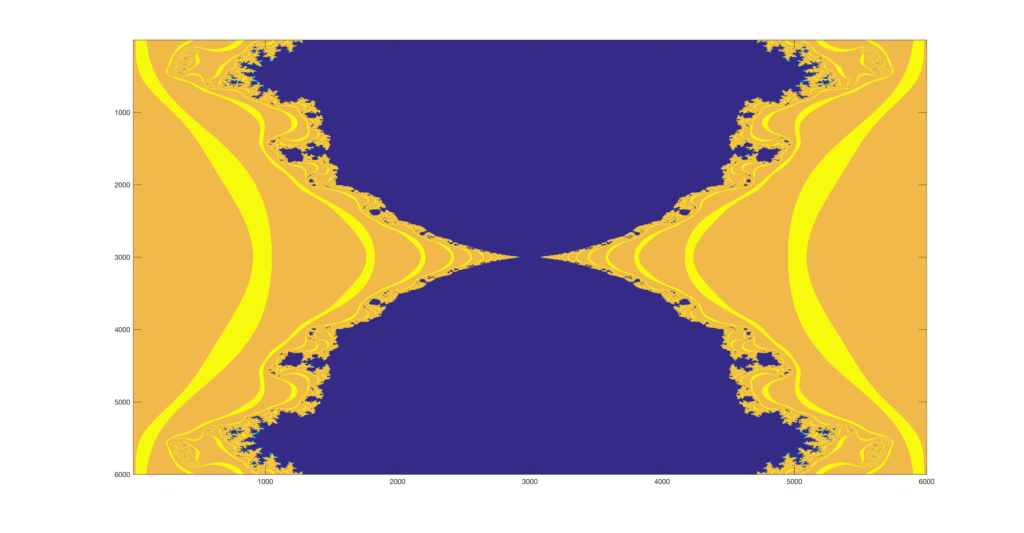
Finally, I decided to try and see how far I could zoom in on the images. I created a function that would be supplied by a point to zoom on and a number of zooming operations, and it then runs the set generator and appends each image to a video file. Below are the results of four points I pseudorandomly selected to zoom in on.

 

Finally, my MATLAB implementation that I used to generate the set. Feel free to use and test this function out as you please, but give me a link if you redistribute it.

function mset_layers = proceduralMandlebrot(dim,iters,bnds)
% proceduralMandlebrot(dim,iters,seeds,bnds)
%
% a function for visualizing the mandlebrot set
%
% dim: the delta_x we discretize by, default 1000
% iters: number of iterations, default 30
% bnds: [x1 x2 y1 y2] limits in the complex plane, default [-2 2 -1 1]
%
% by Majed Samad 2016
t0 = tic;
if ~exist('dim','var')||isempty(dim), dim = 1000; end
if ~exist('iters','var')||isempty(iters), iters = 30; end
if ~exist('bnds','var')||isempty(bnds), bnds = [-2 2 -1 1]; end
[a,b] = meshgrid(linspace(bnds(1),bnds(2),dim),linspace(bnds(3),bnds(4),dim));
x = 0;
c = complex(a,b);
for i = 1:iters
   x = x.^2 + c;
   mset = abs(x)>2;
   if i==1,mset_layers = mset;else mset_layers = mset_layers + mset/i;end
end
imagesc(mset_layers)%,colormap(autumn)
fprintf('it took %f minutes to execute\n',toc(t0)/60);